1.激活函数

sigmoid函数：$\sigma(x)=\sum_{i=1}^n(w_ix_i+b)$：

• 使用了指数，计算量大
• 由于有饱和区域，在输入较大的$x$时，会导致梯度消失（在饱和区梯度为0）
• 当训练数据全为正或全为负时，会导致梯度更新很慢。由于其公式:

$$\sigma(x)=\sum_{i=1}^n(w_ix_i+b)$$

使得计算图中$\sigma$节点处总有$\frac{\partial \sigma}{\partial w}=x$，使得$w$的更新只能向着梯度全为正（或全为负）的方向更新，使得更新效率极低。

解决办法：将数据归一化到均值为$0$的区间内，如$[-1,1]$

tanh函数：$tanh(x)$

• 由于有饱和区域，仍然会导致梯度消失（在饱和区梯度为0）

ReLU函数：$f(x)=\max(0,x)$

• 收敛更快（大概是sigmoid的6倍）
• 在正半轴不会出现梯度消失
• 符合生物学理论

• 计算成本低

• 在负半轴处有饱和区，会有梯度消失（dead ReLU）

• 不是以$0$为中心

参数整流器(PReLU)：$f(x)=\max(\alpha x,x)$

Leaky ReLU：$f(x)=\max(0.01x,x)$

• 在整个实数域上没有饱和区，完全不会出现梯度消失。
• 同时也具有ReLU的优点

ELU函数：

• 表达式为：$f(x)=\begin{cases} x \qquad if \ x>0\\alpha(e^x-1) \qquad if \ x\leqslant0 \end{cases}$

• 具有ReLU的优点

• 对噪音有更强的鲁棒性

maxout函数：$\max(W^Tx_1+b_1,W^Tx_2+b_2)$

maxout的本质相当于是让网络自己学习应该使用什么激活函数。maxout将两个神经元合并成一个（只输出最大值），由于两个神经元的参数都是学习得到的，因此通过参数在学习过程中的变化，两个神经元的输出组合也在不断变化，相当于学习了激活函数。

由于两个神经元都是线性的，因此最终maxout学习得到的激活函数是分段的线性函数（例如也有可能学习到ReLU）

在训练时，假设另一个较小的神经元不存在。

Softmax

一种归一化激活函数，将一个给定向量$K=[k_1,k_2,…k_n]$压缩到另一个向量$K’=[k’_1,k’_2,…k’_n]$，并且使得$K’$中的元素都在$(0,1)$之间，且总和为$1$（类似概率的分布）。任意一个元素$k$的softmax表达式为：

$$k’=softmax(k)=\frac {e^k} { \sum_{i=1}^ne^{k_i}}$$

常常将softmax层放在输出层之前。

权重初始化

• 当网络很深时，不要将权重初始化为很小的值
• Xavier初始化：每层的权重$W_{m,n}$都从标准高斯分布中随机采样，并将结果除以$\sqrt{m}$。即：

  W = np.random.randn(m, n) / np.sqrt(m)
  

• 使用Xavier初始化时，如果对应层使用ReLU函数，需要将$W$除以$2$（因为有一般的输入数据被丢弃）

2. BN（批量归一化）

在网络中加入BN（批量归一化）层。BN层中发生的事情是：对于输入BN层的任意mini-batch，假设该batch中有$N$个样本，每个样本维度为$D$。也即输入数据集$X$的规模为$N\times D$。我们先来看看一般的归一化方法：对于每个维度（每个特征）上的$X$都求均值和方差，并据此对每个维度上的数据进行归一化。对第$k$个维度，归一化之后的数据为：

$$\hat x_k=\frac{x_k-\mathrm{E}[x_k]}{\sqrt{\mathrm{Var}[x_k]}}$$

其中$\mathrm{E}[x_k]$是第$k$维所有$x$的均值，$\mathrm{Var}[x_k]$是第$k$维所有$x$的方差。这一过程通常发生在全连接层或卷积层之后，激活层之前。这么做虽然可以达成归一化的目的，但是一定程度上破坏了之前学习到的数据分布，因此采用以下方法改进：

对于batch中每个维度的数据，引入参数$\gamma_k,\beta_k$。并令它们的初始值为：
$$\gamma_k=\sqrt{\mathrm{Var}[x_k]},\ \beta_k=\mathrm{E}[x_k]$$

改进版的归一化中，我们使用$y_k=\gamma_k\hat{x}_k+\beta_k$来进行归一化操作。其中$\hat{x}_k$是刚才普通归一化得到的结果。之前提到，$\hat{x}_k$可能会导致数据分布损失，但是经过$y_k=\gamma_k\hat{x}_k+\beta_k$，$y_k$的值可以把归一化后的数据还原到原始数据，这样就保证开始训练时，之前的学习成果不会因为归一化而丢失。

与此同时，随着训练的进行，$\gamma_k,\beta_k$的值也会进行根据梯度下降进行调整，这样就可以使得数据从原始数据开始，逐渐归一化为符合高斯分布的数据，并将数据通过缩放和平移，变换到一个便于计算的区域，这样就既保存了之前的学习成果，又方便了之后的处理。妙蛙！(๑•̀ㅂ•́)و✧

3. SGD的优化方法

普通SGD（$w^{new}=w-\alpha \nabla f(x)$）缺点：

• 会陷于局部极小值（鞍点）
• 梯度方向不与全局方向相同
• 部分样本的梯度与总体梯度不一定相同

类似一个小球以十分不科学的均匀速度滚下山，而且每个时刻的速度方向都是向着当前的最陡峭方向

动量法(Momentum)

在梯度项后加入一个动量（速度）项，速度的方向就是前一步的梯度方向：

$$v^{new}=\nabla f(x)+\rho v,w^{new}=w-\alpha v^{new}$$

v的初始值为0，在每次迭代中更新。$\rho$是摩擦系数（超参数，通常取$0.9$）。类似一个小球滚下山，但速度越来越快，由于引入摩擦系数，可以保证最终停在山脚（感觉科学了一些呢）。这样可以在“惯性”的作用下越过鞍点，收敛速度也更快。

Nesterov动量（Nesterov Momentum）

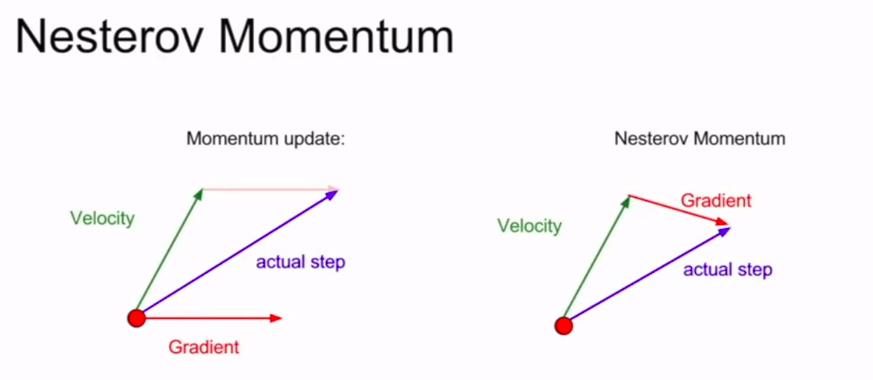
在某一点处，假设向着当前速度行进一段时间后，计算出行进后某点处的梯度方向，然后将二者合成，作为当前实际的前进方向:

$$v^{new}=\rho v-\alpha \nabla f(x+\rho v),w^{new}=w+v^{new}$$

AdaGrad

在迭代过程中把每一步计算得到的梯度平方项累加，并把计算后的梯度除以当前的累加项：

$$S^{new}=S+(\nabla f(x))^2,w^{new}=w-\alpha \frac{\nabla f(x)}{S^{new}}$$

优点：可以避免梯度下降时对各个维度的$w$敏感程度不同（感觉有些类似归一化）
缺点：导致步长越来越小，容易困在局部极值点。因此一般不使用AdaGrad，而用改进的方法：

改进：RMSprop

在累加平方项的过程中，同时使得每次累加的值不断减小，这样就保证了步长不会随着训练而减小过多：

$$S^{new}=\rho S+(1-\rho)(\nabla f(x))^2,w^{new}=w-\alpha \frac{\nabla f(x)}{S^{new}}$$

其中$\rho$是衰减率，使得累加项的增幅逐渐减小。

Adam算法（动量+RMSProp）

结合了二者的优点，在每次迭代时计算出动量项和梯度平方的累加项，并综合二者信息进行权重更新。

二阶优化

1.牛顿法

假设loss函数$E(x)$是一个$N$维的实值函数（从$N$维空间到实数的映射），把求该函数的极值点的问题，转化为求$E’(x)=0$的问题。在每次迭代中，使用二次函数拟合损失函数（即二项泰勒展开），找到展开后的二次函数的极值点，直接将其当做新的权重，由此不断进行优化。

在实际计算中，假设在$x_0$点处进行迭代，$E’(x)$是$E(x)$关于$x$每一个维度求导数，是$n\times 1$的向量。$E’’(x)$是$E(x)$关于$x$任意两个维度求导数，因此$E’’(x)$是$n\times n$的矩阵，称为海森矩阵（设为$H(x)$）。泰勒展开并解方程，可以得到在$x_0$处牛顿法更新的表达式：

$$x=x_0-H^{-1}(x_0)E’(x_0)$$

其中令$-H^{-1}(x_0)E’(x_0)=d$称为牛顿法的迭代方向。

2.拟牛顿法

由于牛顿法每一次迭代就要计算二阶导数并求逆，计算较为复杂，因此使用一个近似的矩阵$B$和$D$来逼近$H$和$H^{-1}$。

要拟合海森矩阵，就要知道它满足的条件，并以此作为依据来进行拟合。假设在第$k$次迭代过程中的$x$值为$x_k$，那么将$x$在$x_{k+1}$处泰勒展开，并对等式两边应用哈密尔顿算子（即$\nabla$），可以得到关于$H$的方程，将$x_k$代入方程（即把$f(x_k)$在$x_{k+1}$处展开），可以得到拟牛顿法需要满足的条件：

$$x_{k+1}-x_k=H_{k+1}^{-1}(\nabla f(x_{k+1})-\nabla f(x_k))$$

只要根据这个条件迭代更新矩阵$B,D$，就可以认为最终得到的结果与$H,H^{-1}$在性质上近似。为了消除牛顿法收敛不稳定的特性，常常采用阻尼牛顿法：
在迭代方向$d$上寻找一个最优的步长$\lambda$进行迭代。即：

$$\lambda=arg\min_{\lambda \in \Bbb R}f(x+\lambda d)$$

常用的拟牛顿法有：

• DFP算法：$B,D$初始化为单位矩阵，通过待定法推导得出迭代公式：

  $$D_{k+1}=D_k+\frac{s_ks_k^T}{s_k^Ty_k}-\frac{D_ky_ky_k^TD_k}{y_k^TD_ky_k}$$

  其中$s_k=\lambda_k d_k,y_k=\nabla f(x_{k+1})-\nabla f(x_k)$

• BFGS算法：思路与DFG算法大致相同，只是$s_k,y_k$的位置呼互换，推导过程相似。得出迭代表达式：
  $$D_{k+1}=(I-\frac{s_ky_k^T}{y_k^Ts_k})D_k(I-\frac{y_ks_k^T}{y_k^Ts_k})+\frac{s_ks_k^T}{y_k^Ts_k}$$

  其中$y_k,s_k$与之前相同。

• L-BFGS算法：由于存储$D_k$的开销巨大，因此存储m组$s,y$，即$(s_k,y_k),(s_{k-1},y_{k-1}),…(s_{k+1-m},y_{k+1-m})$，并用它们来表示$D_k$。但是由于用到多组$s,y$，使得$D_k$的表达式十分复杂，因此使用快速计算$D_k\nabla f(x_k)$的算法，算法详情见论文：Updating Quasi-Newton Matrices with Limited Storage

4.抗过拟合

正则化

在损失函数后加入一项正则项，作用是作为“惩罚项”，抑制了模型参数的复杂度。常用的有$L_1$正则化和$L_2$正则化：

• $L_1$正则项：所有参数的绝对值之和，可以表示为参数向量$W$的$L_1$范数：$\lambda||W|| _1 = \lambda \sum_{i=1}^n|w_i|$
• $L_2$正则化：表示为参数向量$W$的$L_2$范数：$\lambda||W||_2^2 = \lambda \sum_{i=1}^n w_i^2$

集成学习

在不同训练集上训练不同的模型，最后对多个模型集成，得到一个平均的模型。（不同模型超参数有时也会不同）

Dropout

神经网络每次正向传播经过某一层时，随机将该层中的某些神经元的激活函数置0（相当于暂时丢弃这些神经元），要注意每次传播经过每一层丢弃的神经元都时随机的，并且置零的神经元数目根据dropout的概率$p$决定。一般在全连接层进行dropout。另一种解释是，dropout相当于在一个网络中集成学习。

进行测试时，每个神经元表示为$y=f(w,x)$，假设输入$x$由$n$个神经元的输出组成，经过dropout之后，该神经元的输入$x$中的$n$项有$m$项被丢弃了，由于在训练中这些项是被随机丢弃的（假设每个神经元被丢弃的概率为$p$），因此在训练时需要记录下被丢弃的神经元，并计算出该神经元$y$的输出的期望值，在测试时使用期望值代替实际值（例如，假设每个神经元都有$p=0.5$的概率被丢弃，那么$y=0.5\sum_{i=1}^nw_ix_i$）。另一种方法是，在训练时除以概率$p$，测试过程保持不变，可以达到相同的效果(反转dropout)

使用dropout会导致训练时间变长，但是训练后的鲁棒性更好。

随机扰动

dropout和BN使用的其实都是这种思想。其他使用随机性方法的例子还有：

• 对图片随机裁剪，翻转
• 使用色彩抖动，例如随机改变对比度和亮度
• 类似dropout，随机将网络中的一些权重设置为0，相当于暂时切断部分神经元之间的连接。
• 部分最大池化：随机池化部分区域
• 随机深度：在训练时随机丢弃一些层，在测试时使用全部层。

5. 生成模型

Pixel RNN

该模型的初始输入是图片的第一个像素（初始像素）（如果是RGB三通道，那么每个像素包含三个数字），输出下一个像素；然后输入初始像素和生成的像素，得到下一个像素…每一次的输入都包含之前所有的像素，不断循环得到整张图片。

也可以用在语音合成和文字和影像生成上。

自动解码器（AE）

$$\text{原图片} \stackrel {encode}{\longrightarrow} code \stackrel {decode}{\longrightarrow} \text{生成图片}$$

通过训练使得生成的图片更接近于原图片，训练完成后输入一个随机的$code$向量，通过$decode$就可以得到生成的图片。

改进：变分自动解码器（VAE）

不直接生成$code$向量，而是生成三个向量$m,\sigma$，再从一特定分布中取一向量$e$，通过$code=exp(\sigma)\times e+m$得到$code$。其他和$AE$相同。

训练完毕后，如果在生成过程中人为指定$code$向量的某些维度，得到的图片中会有某些共同性。可以认为，$code$中的维度具有控制图片性质的功能，具有某些特定的含义。

原理：假设所有的真实样本都符合高斯混合分布，是从某一个由高斯混合模型中生成的，$VAE$通过极大似然来估计获得该模型的参数，即通过高斯混合模型来拟合真实的数据（记为$x$）分布。高斯混合模型（记为$G$）是由多个不同的高斯模型$g_1,g_2,…g_n$组合得到，初始的噪声$code$（记为$z$），其实包含的就是 选择哪些$g_i$，以及从这个高斯模型中的那个地方采样，采样结果组合起来就得到了生成的样本。

具体如何得到这个高斯混合模型$G$，也即如何从$z$得到各个$g_i$的参数$\sigma, \mu$，方法就是通过神经网络$decoder$来拟合不断拟合$G$的分布。也即，训练$decoder$的过程就是求$decoder$中的参数对$P(x)$的最大似然。而此时:

$$P(x)=\int_{z}P(z)P(x|z)$$

即真实数据的概率分布等于，在向量$z$中选择一个初始值$z$（这个值用来控制选择哪个高斯模型的哪个位置采样），概率为$P(z)$，并且在给定一个初始值$z$的情况下，$G$生成真实样本$x$的概率，即$P(x|z)$。对于每个这样的初始值$z$，模型进行一次采样，将所有采样的结果叠加，概率为$\int P(x)$

通过数学推导，$L = logP(x) = L_b + KL(q(z|x)||p(z|x))$，$L$表示似然，也即$L$由$q(z|x),p(z|x)$的$KL$散度（一种衡量概率分布之间的关联性的量）以及一个$L_b$组成，由于$KL>0$，因此$L_b$就是似然的下界。

在实际的操作中，往往通过最大化该下界，来使得$L_b$尽可能接近$L$，即尽可能最小化$KL$散度，使得$KL=0$。通过同时最小化$KL$以及最大化$E_{q(z|x)}[logP(x|z)]$，就得到了$VAE$的损失函数。

缺点：只是单纯地使得输出的结果和数据集中的某些图片越接近越好，有时只是数据集中不同样本的简单组合。