大家有想补充或者更正的,可以跟我说或者自己加上去,或者考虑分成多篇
一些问题
极大似然与负对数损失
极大似然中,一组参数在一堆数据下的似然值,等于每一条数据在这组参数下的条件概率之积。
而我们通过模型得到的置信度,其实就是那个条件概率,所以我们的目标是让他们的积最大。
但损失函数一般是每条数据的损失之和,为了把和变为上面的积,就对每一项取了对数。让对数之和最大,其实就是让负对数之和最小。于是我们便有了负对数损失(NLL Loss)。
$$L(y) = -\log(\hat{y_i})$$
注意:pytorch中的NLLLoss本身不进行对数运算,只做一个取负
负对数损失与交叉熵损失的关系
交叉熵损失定义如下,其中$Y$为真实label(0/1),$\hat{Y}$为预测的结果
$$H(Y,\hat{Y})=-Y\cdot \log (\hat{Y})=-\sum_i y_i \cdot \log (\hat{y_i})$$
将最右边的式子展开,得到的其实就是负对数损失。
softmax与交叉熵
softmax中的$e^x$与交叉熵中的$\log(x)$抵消,使模型易于收敛。
因此softmax通常作为输出层的激活函数
注意:pytorch中的CrossEntropyLoss自带softmax
为什么要用softmax
- 当使用交叉熵损失时softmax中的$e^x$与交叉熵中的$\log(x)$抵消,使模型易于收敛。
- 我们希望特征对概率的影响是乘性的,即各个部分的概率相乘得到最后的概率。但在我们模型中各个概率是相加的,所以以指数的形式将其改为相乘关系。
- softmax满足最大熵原则。即在满足一系列限制条件的情况下,对一个多分类问题,没有任何先验知识的系统,最公正的,也就是最没有偏私,才能让不确定性最大,这就必然导致概率分布满足boltamann形式,也就是softmax。
一些术语
下面主要记录一些基础的术语
信息论&概率论
熵(Entropy)
熵在信息论中可以理解为,一个事件包含的信息量。熵越小,事件包含的信息量就越小。必然事件和不可能事件的熵为0(比如“我是我妈生的”这句话为必然事件,不包含任何信息,信息量为0)。熵定义如下:
$$S(x) = -\sum_i P(x_i) \log_b P(x_i)$$
其中S为熵,x为事件,当x必然发生或必然不发生时,$P(x)$为1或0,此时S为0。
KL散度/KL距离/相对熵(relative entropy)
KL散度一般用来计算两个概率分布之间的距离,但它与普通的距离计算不同,因为’A对B的KL距离’不一定等于’B对A的KL距离’。
对离散事件: $D_{KL}(A||B) = \sum_i P_A (x_i) \log \frac{P_A (x_i)}{P_B(x_i)} )$
对连续事件: $D_{KL}(A||B) = \int a(x) \log \frac{a(x)}{b(x)}$
如果A与B的概率分布相同,即$P_A=P_B$,则距离为0。
交叉熵(Cross Entropy)
交叉熵同样用来衡量两个分布之间的差异,其定义如下:
$$H(A,B)= -\sum_i P_A (x_i) \log (P_B (x_i))$$
可以推出来 $D_{KL}(A||B) = -S(A)+H(A,B)$
互信息(mutual information)
直观上理解,互信息度量X与Y之间共享的信息量。
若 p(x,y) 是X和Y的联合概率分布函数,而p(x)和p(y)分别是X和Y的边缘概率分布函数。则X与Y的互信息定义为:
对离散事件: $I(X;Y) = \sum_{x \in X} \sum_{y \in Y} p(x,y)\log (\frac{p(x,y)}{p(x)p(y)})$
对连续事件: $I(X;Y) = \int_Y \int_X p(x,y) \log (\frac{p(x,y)}{p(x)p(y)})$
它其实就是计算了联合概率分布与边缘概率分布乘积之间的KL距离。
$$I(X;Y)=D_{KL}(p(x,y)||p(x)p(y))$$
交叉熵与KL散度的关系
- 相同点:a. 都不具备对称性 b. 都是非负的
- 当$S(A)$固定时,最小化KL散度与最小化交叉熵等价。而交叉熵公式更简洁,因此我们一般都使用交叉熵。
在机器学习中,我们要让模型的分布逼近数据集的分布,而数据集就是上面的A,因此$S(A)$固定
距离度量
欧氏距离(Euclidean distance)
$$d_{12} = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$$
曼哈顿距离(Manhattan Distance)
$$d_{12} = |x_1-x_2|+|y_1-y_2|$$
闵可夫斯基距离(Minkowski Distance)
可以看做是欧氏距离和曼哈顿距离的一种推广
$$d_{12} = \sqrt[p]{(x_1-x_2)^p+(y_1-y_2)^p}$$
当$p=1$时,就是曼哈顿距离
当$p=2$时,就是欧氏距离
当$p \to \infty$时,就是切比雪夫距离
马氏距离(Mahalanobis Distance)
前面的距离度量均会受到变量量纲的影响,而马氏距离通过对数据的仿射变换,消除了这种影响。这是它的优点,而在某些情况下也会成为它的缺点。
定义:有m个样本向量$X_1, X_m$,协方差矩阵记为S,则其中向量$X_i$与$X_j$之间的马氏距离定义为:
$$D(X_i,X_j) = \sqrt{(X_i-X_j)^TS^{-1}(X_i-X_j)}$$
余弦距离(Cosine Distance)
与欧氏距离相比,余弦距离对各个特征之间的相对大小更为敏感,对绝对大小却不怎么敏感。在人脸检索等领域,貌似余弦距离与欧氏距离表现差不多?不过毕竟欧氏距离更直观,所以除一些特定问题外还是用欧氏距离吧。
对它比较有兴趣的可以看看这个
编辑距离(Levenshtein Distance)
用来定义两个字符串之间的距离,指两个字串之间,由一个转成另一个所需的最少编辑操作次数。Standardization字符,删除字符。
杰卡德距离(Jaccard Distance)
用于衡量集合间的距离,定义为两集合的交集与并集中元素数量的比值。物体检测中的IoU其实就是杰拉德距离。
$$J(A,B) = \frac{|A\bigcap B|}{|A\bigcup B|}$$
数据预处理
归一化(Normalization)
通过对原始数据进行线性变换把数据映射到[0,1]之间
$$x’ = \frac{x-min}{max-min}$$
标准化(Standardization)
使数据均值为0,标准差为1
$$x’ = \frac{x-\mu}{\sigma}$$
评价标准
首先定义基本的评价标准
| | 预测为真 | 预测为假 |
| :—: | :—: | :—: |
| 实际为真 | TP(真正例) | FN(假反例) |
| 实际为假 | FP(假正例) | TN(真反例) |
接下来的评价标准基本都基于上面这四个
精确率/查准率(precision)
$$P = \frac{TP}{TP+FP}$$
召回率/查全率(recall)
$$R = \frac{TP}{TP+FN}$$
准确率(accuracy)
$$Acc = \frac{TP+TN}{TP+FP+TN+FN}$$
F1 Score
通常我们需要综合精确率和召回率进行考虑,这时我们一般使用F1度量
$$F_1 = \frac{2 \times P \times R}{P + R} = \frac{2 \times TP}{2 \times TP + FP + FN}$$
当对精确率和召回率的重视程度不同时,我们可以采用更一般的$F_\beta$
$$F_\beta = \frac{(1+\beta^2) \times P \times R}{(\beta^2 \times P) + R}$$
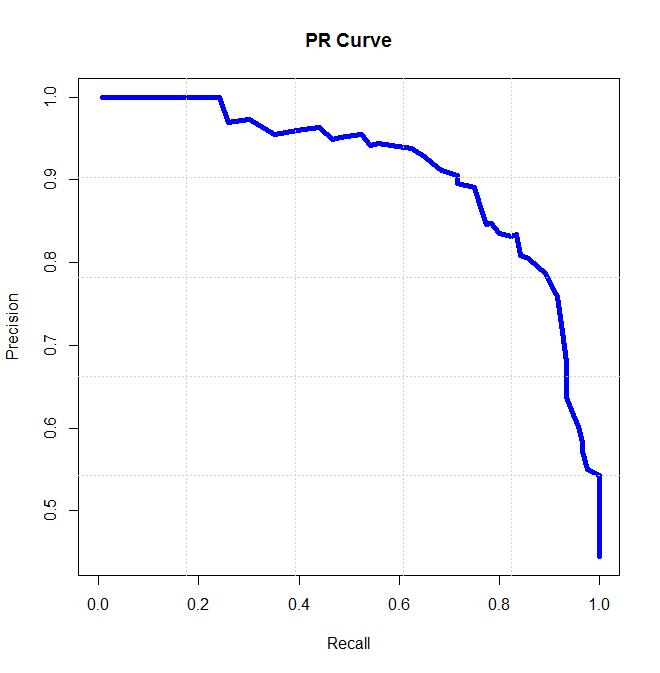
P-R曲线
以召回率为横轴,精确率为纵轴,得到的曲线为P-R曲线。
当对两个模型进行比较时,我们可以根据他们P-R曲线下的面积(AP)判断,面积越大性能越好。
ROC曲线
先定义真正例率和假正例率:
$$TPR = \frac{TP}{TP+FN}$$
$$FPR = \frac{FP}{TN+FP}$$
以FPR为横轴,TPR为纵轴即可得到ROC曲线。
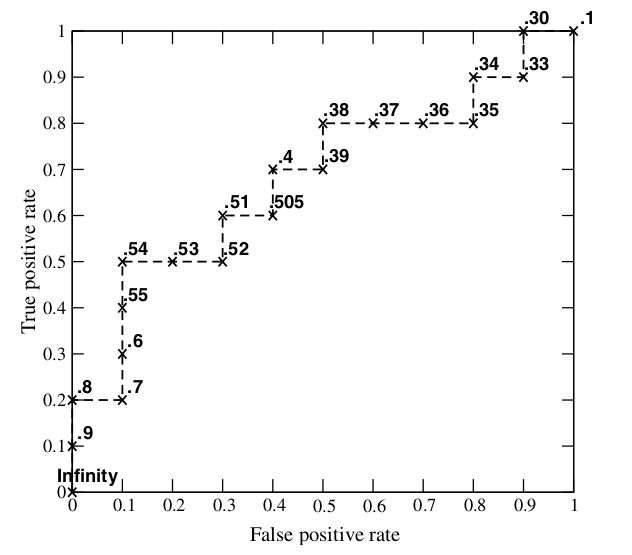
AUC
ROC曲线下的面积即为AUC,越大说明模型越好。可以无视正负样本不平衡的影响
mAP(mean average precision)
常用于多类别物体检测。对每个类别均可以绘制一条P-R曲线,其中AP即指P-R曲线下的面积。mAP即为多个类别AP的平均值。
奇怪的卷积
反卷积/转置卷积 (deconvolution / transposed convolution)
可以理解为一种特殊的卷积,只不过它会将feature map放大,达到上采样的效果。
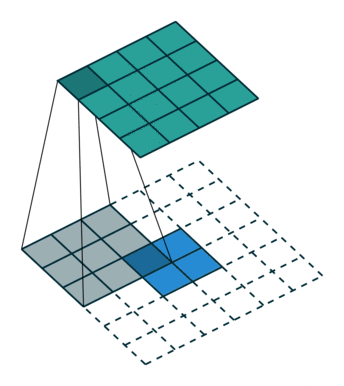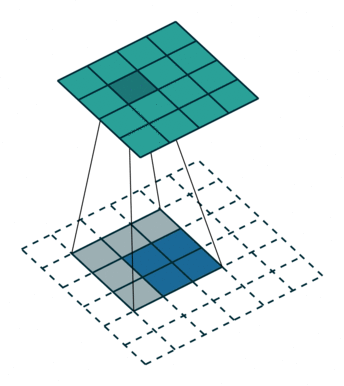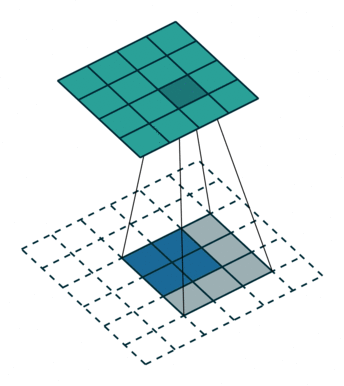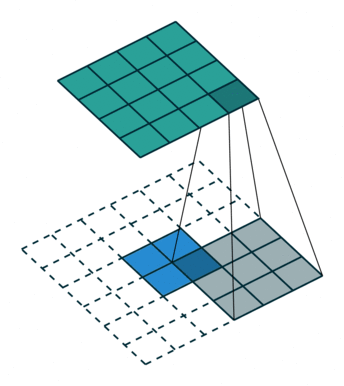
上图可以理解3x3的卷积核,padding=2,stride=1的卷积操作。而同时,在特征图大小变化上,与padding=0,stride=1的卷积操作相反。
用pytorch实现时代码如下,其中kernel_size为3,stride与padding按其对应的卷积操作参数进行设置。
1 | torch.nn.ConvTranspose2d(in_channels, out_channels, kernel_size, stride=1, padding=0) |
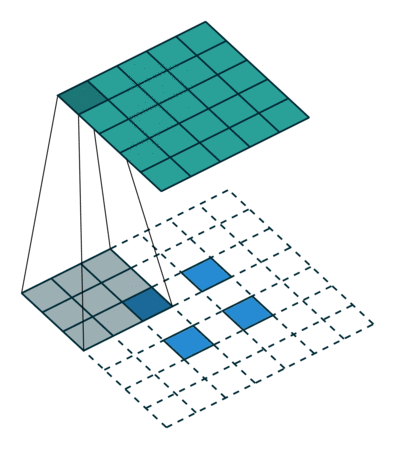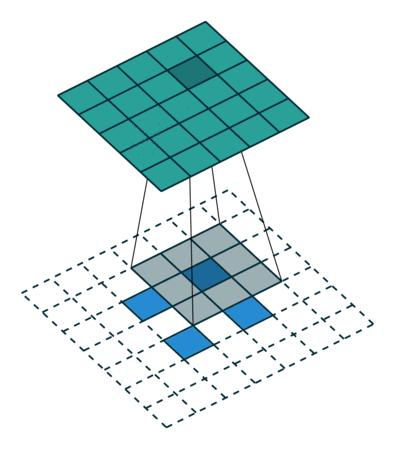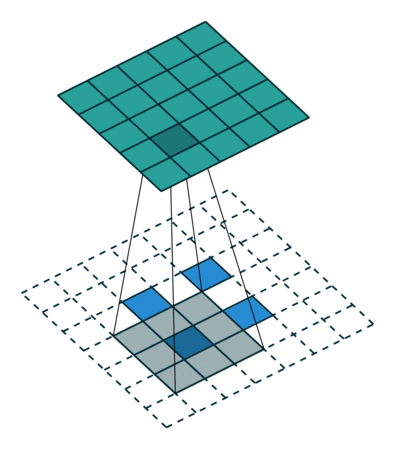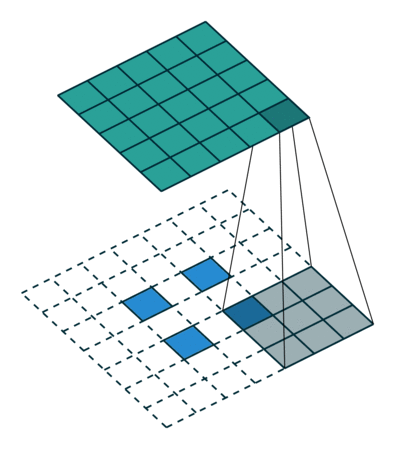
当卷积操作stride大于1时,此时其对应的转置卷积的stride小于1,此时被称为分数卷积(fractionally-strided convolution),如下图:
空洞卷积/扩张卷积(Dilated Convolutions)
空洞卷积可以在基本不增加计算量的前提下,增大感受野。之前如果需要扩大感受野,都是采用池化,但池化会造成分辨率下降。
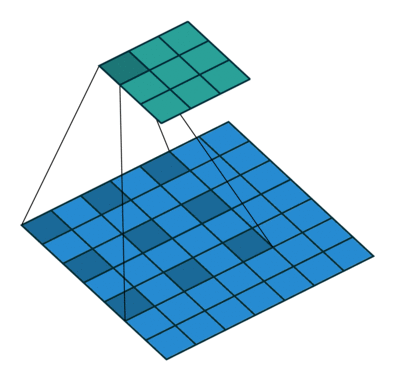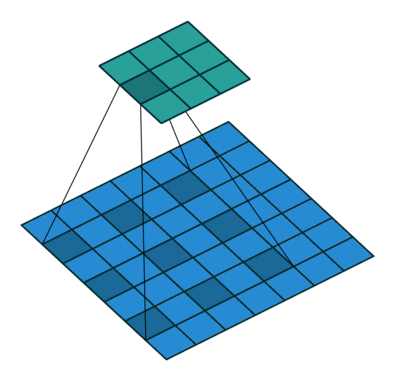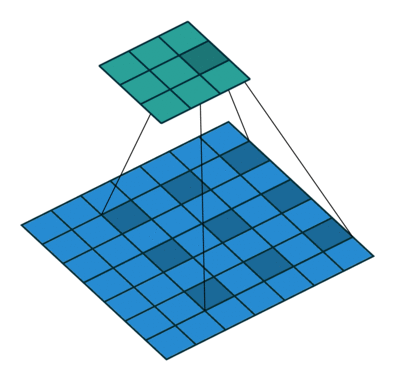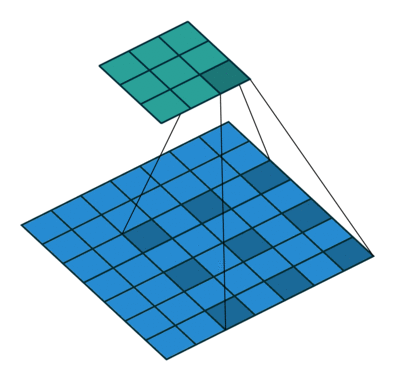
为了不损失数据的连续性,我们需要选择适当的各层空洞卷积参数,如下图的配置方案。
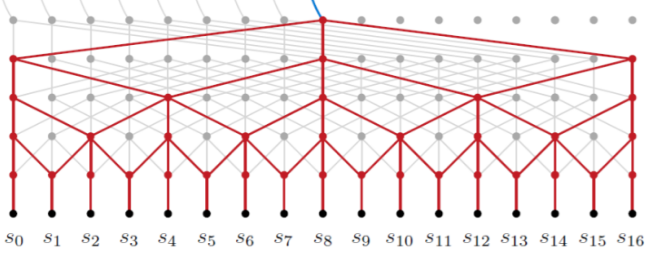
pytorch中实现有一个空洞的卷积操作,代码如下:
1 | torch.nn.Conv2d(in_channels, out_channels, kernel_size, stride=1, padding=0, dilation=2) |
其中dilation参数默认为1,为1在pytorch中定义为没有空洞。不同框架中对此参数的定义不同,需要注意。
空洞卷积感受野大的特点使其可以处理长序列问题,甚至可以达到和RNN相差无几的效果。
可变形卷积(Deformable Convolutions)
TODO
深度学习的各种归一化
BN/LN/IN/GN/SN
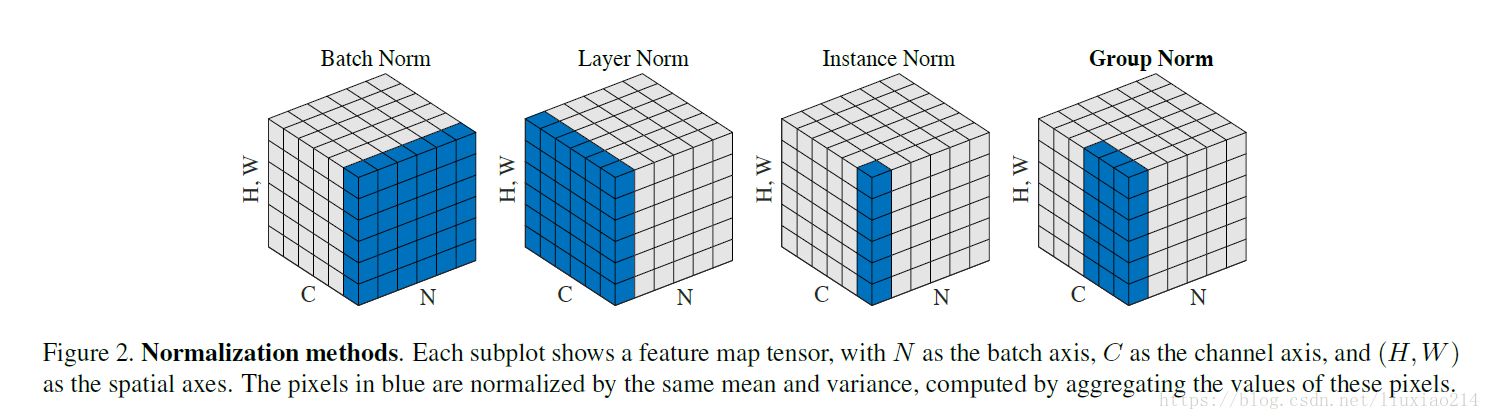
- batchNorm是在batch上,对NHW做归一化,对小batchsize效果不好;
- layerNorm在通道方向上,对CHW归一化,主要对RNN作用明显;
- instanceNorm在图像像素上,对HW做归一化,用在风格化迁移;
- GroupNorm将channel分组,然后再做归一化;
- SwitchableNorm是将BN、LN、IN结合,赋予权重,让网络自己去学习归一化层应该使用什么方法。
机器学习问题
维数灾难
维数(特征)增多主要会带来的高维空间数据稀疏化问题,即有限的数据在高维空间下更稀疏。当数据维度增高,各个维度之间可能的组合数呈指数增长,我们所拥有的数据覆盖了一部分组合,但其覆盖的百分比越来越小。所以当数据维数(特征)较多而数据较少时易造成过拟合。
同时,高维空间下,距离计算更加困难,而且最大与最小欧氏距离之间的相对差距会越来越小($\lim_{d \to \infty} \frac{D_{max}-D_{min}}{D_{min}} \to 0$),所以收敛会变慢。
实践
预处理一般步骤
一般需要对数据进行:
- 去除无用属性,如每个人的id
- 填补缺失值
- 特征编码,对非数值特征进行独热编码(若此特征只有两种取值,可以直接0/1)
- 数据标准化
- 打乱数据
- 可能需要降维
- 划分训练集、验证集、测试集
提高最终结果
- bagging/boosting大法
- 图片金字塔:对检测等任务,可以将图片缩放为不同大小再输入,最后综合多个结果
训练技巧
预训练
使用别人预训练的模型时,最好要保证自己的数据分布与别人的数据分布一致,比如对于图片分类,若用imagenet预训练模型,最好先将图片每个channel标准化
batchsize大小
一般来讲:
- batchsize越大,训练越稳定
- 在一定范围内,增大batchsize不会增加每个batch的运算时间
- 小batchsize相比大batchsize,相当于在每个iter中增加了噪声,起到一定的正则化效果,可以减小泛化误差。但同时为了维持稳定,需要更小的学习速率,训练更慢
提速
- GPU占用率<<100%通常表明,此时系统在对数据进行读写或预处理。若这部分时间占用较大,可以考虑提前进行不带随机数的预处理(如转化为灰度图、resize等),并将结果以.pkl文件保存。可以减少IO及预处理时间
- 在内存足够的情况下多进程读取数据
- 可以尝试去寻找一个合适的绝对最小批量,batchsize低于它时,不会减少每个batch的运算时间。- 同时batchsize为2的幂时可能会较快
可能存在的误区:训练快慢并不能只看每个epoch需要多少时间,当batchsize增大,每个epoch所需时间减少,但每个epoch内的iter次数(参数更新次数)也减少,不一定收敛快。一般在保证每个iter所需时间几乎最短的情况下增大batchsize即可。
模型保存
- 日常训练时暂存模型,尽量使用框架提供的方法,仅保存参数。当得到一个较好的模型时,可以考虑将其以.pkl形式保存一份(若定义网络模型的代码有改动,只保存参数会导致无法方便的把参数加载进去)
- 保存模型参数时一般同时保存当前的epoch数、优化器的参数
延拓法
使用多个损失函数,可以让模型不那么容易被限制在局部最小值点。