填个强化学习入门的坑~
Step 1: 基础的概念
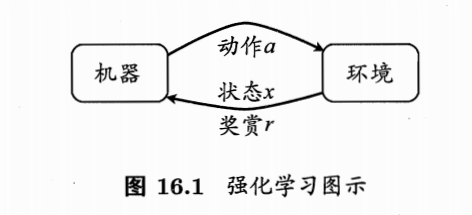
- 引入一些基本的概念
- $E \space (Environment) $ :环境,即机器所处的环境
- $X$ 或 $S(State)$:机器所处的状态空间,即所有空间构成的集合,$x $ 或 $s$ 为机器感知到的环境的描述
- $A(Action)$ :动作空间,即机器所有能采取的动作的集合, $a$ 为机器采取的具体的动作
- $P$ :动作背后潜在的转移函数,能使作用在当下状态 $s$ 的动作 $a$ 使环境从当前状态按某种概率转移到另一个状态。
- $R(reward)$:奖赏,即状态变化的时候反馈给机器的信息,可正可负
- 综上所述,一个强化学习对应了一个四元组 $E$ = $\langle X,A,P,R \rangle$
- 我们学习的目的是通过不断地尝试学的一个策略 $\pi (policy)$ ,根据策略有 $a = \pi (x)$
- 策略有两种表示:确定性策略:$\pi : X {\rightarrow} A $ ,另一种是随机性策略$\pi : X\times A \rightarrow \mathbb R $ ,$\pi(x,a)$代表状态 $s$ 下 选择 $a $ 的概率,自然有 $\sum_a \pi(x, a) = 1$
- 我们用执行策略后的得到的累计奖赏来评估策略的优劣。学习的目的就是找到使长期累积最大化的策略。
Step 2: 从“最大化单步奖赏开始”
- 和监督学习相比,强化学习的一个最大的特征就是最终奖赏有延时性,可以把强化学习看作具有”延迟标记信息“的监督学习问题。我们不妨先从一个简单的情形开始讨论:最大化单步奖赏(这和我们的现实情况还是有很大差别的)
如何最大化单步奖赏? 我们给出如下的考虑
- 知道每个动作带来的奖赏
- 执行奖赏最大的动作
- 简单情况是每个动作的奖赏是一个确定值
- 更普遍的情况是奖赏来自于一个概率分布,一次尝试不能确切地获得平均奖赏
- 我们用”K-摇臂赌博机“来对应这种问题:”如图所示,赌徒投入一个硬币后,选择一个摇杆,每个摇杆有一定的概率吐出硬币,这个概率赌徒并不知道。赌徒的目标就是通过找到一个策略来使自己在等量成本下,收益最大”。
- 我们可以先考虑两种极端的思路:
- Exploration-only(仅探索):把所有的尝试机会平均分给每个摇臂(轮流按下每个摇臂),最后将得到的平均概率作为奖赏期望的近似估计。这样虽然能获得每个摇臂近似的奖赏,但是做不到收益最大。
- Exploitation-only (仅利用) : 只按目前最优的摇臂(目前为止平均奖赏最大的)。这样无法判断每个摇臂的奖赏,当前最优很可能和全局最优不同,也不能保证收益最大。
- Exploration vs Exploitation :显然,在尝试次数有限的情况下,双方是相互矛盾的(即探索-利用窘境:Exploration -Exploitation dilemma)。想要奖赏最大,必须有所折中
于是我们引入:$\epsilon$ - greedy ($\epsilon$-贪心)是一种基于概率折中两者的算法:

基本思路:每次尝试时,以 $\epsilon$ 的概率进行探索,以均匀概率随机选取一个摇臂,以 $1-\epsilon$ 的概率进行利用,即选择当前平均奖赏最高的摇臂
关于如何记录平均奖赏,最简单的是记录每个摇臂获得的奖赏取平均,但是需要记录若干个奖赏值,对计算空间有一定要求。于是我们采取增量式来记录平均奖赏:
$$Q_n(k) = \frac{1}{n}((n-1)\times Q_{n-1}(k) + v_n)$$
(其中 $Q_n(k)$ 为摇臂k的n次尝试后的平均奖赏,$v_n$为第n次获得的奖赏) ,此后只需要记录 $Q_n(k) $ 和 $v_n$ 的值。
引入算法

一些说明:
- 当奖赏的不确定性较大时(概率分布较宽),需要更多的探索,即更大的 $\epsilon$ ;类似的,概率分布集中时,则需要更小的 $\epsilon$
- 若尝试次数非常大,在一段时间后,每个摇臂的奖赏都能很好的近似出来,不再需要探索,此时可以设置 $\epsilon = 1/ \sqrt{t}$ (笔者亲测这个效果非常好)
此外我们还可以使用softmax算法:
- 我们不直接设置探索和利用的概率,而是通过计算不同 $k$ 各自 $Q(k)$ 的占比来判断,选取哪一个摇臂,我们有 $$P(k) = \frac{e^{\frac{Q(k)}{\tau}}}{\sum_{i=1}^{K} e^{\frac{Q(i)}{\tau}}} $$ 其中,$\tau$ 为“温度”,$\tau$ 越小,则平均奖励高的摇臂被选取的概率越高,$\tau$ 趋于0时,Softmax将趋于“仅利用”,$\tau$ 趋于无穷大时, Softmax将趋于”仅探索”
- 引入算法

- 至此我们对如何单步奖赏最大化已经有了一定了解,接下来我们转入多步强化学习任务。
Step 3: 从模型已知的学习任务(有模型学习)开始
- 在现实世界中,绝大多数的学习任务都是没有固定模型的,即上面提到的环境中参数是未知的。即所谓的“免模型学习 (model-free learning) ”;与之对应的则是知道环境参数的学习:“有模型学习(model-based learning)”。我们先从有模型学习开始,来讨论一些在强化学习中十分重要的结论。
- 此部分涉及到复杂的数学推导,阅读时可以注重推导出的结论而非过程
先列一下有模型学习中已知的参数:
- $P_{x \rightarrow x’}^a$ 已知,即已知对于任意状态 $x$,$x’$和动作 $a$, 在 $x$ 状态下执行动作 $a$ 转移到 $x’$ 状态的概率(状态转移概率已知)
- $R_{x \rightarrow x’}^a$ 已知,即已知上述状态转移带来的奖赏
- 最后不妨假设状态空间 $X$ 和 动作空间 $A$ 是有限的
我们再引入一些研究对象:
- $V^{\pi}(x)$: 代表从状态 $x$ 出发后,使用策略 $\pi$ 带来的累计奖赏。
- $V(\cdot)$ 称为“状态值函数(state value function)”
- $Q^{\pi}(x,a)$: 代表从状态 $x$ 出发后,执行动作 $a$ 后**使用策略 $\pi$ 带来的累计**奖赏。
- $Q(\cdot)$ 称为“状态-动作值函数(state-action value function)”
- $V^{\pi}(x)$: 代表从状态 $x$ 出发后,使用策略 $\pi$ 带来的累计奖赏。
为了得到最优的算法,我们先讨论策略评估,即如何评估我们的算法
策略评估
- 我们先尝试给出$V^{\pi}(x)$的式子:(其中 $r_t$为第 $t$ 步获得的奖赏)
$$\begin{cases}
V^{\pi}_T(x) = \mathbb E_{\pi}[\frac{1}{T} \sum_{t=1}^T r_t | x_0=x]\
V^{\pi}_\gamma (x) = \mathbb E_{\pi}[\sum_{t=0}^{+\infty}\gamma ^tr_{t+1} | x_0=x]\
\end{cases}
$$ - 以上两个式子分别是根据 $T$ 步累计奖赏和 $\gamma$ 折扣累计奖赏展开的,计算了前 $T$ 步奖赏的期望和按 $\gamma$ 衰减奖赏的期望。同样的我们有
$$\begin{cases}
Q^{\pi}_T(x,a) = \mathbb E_{\pi}[\frac{1}{T} \sum_{t=1}^T r_t | x_0=x,a_0=a]\
Q^{\pi}_\gamma (x,a) = \mathbb E_{\pi}[\sum_{t=0}^{+\infty}\gamma ^tr_{t+1} | x_0=x,a_0=a]\
\end{cases}
$$ - 和上面状态值函数的区别在于初始条件增加了$a_0=a$
考虑到系统下一时刻的状态只和当前状态有关,不依赖以往任何状态,于是我们可以通过递归展开进一步计算 $V^{\pi}_T(x)$。
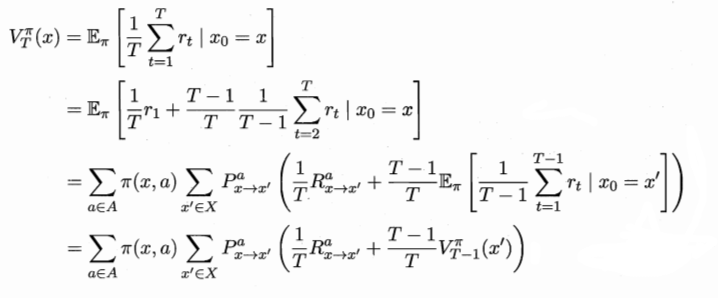
- 这个式子中,变量在于 $\pi(x,a)$,即我们选择的策略,而非$V_T^{\pi}(x)$中的初始状态 $x$,值函数关注的不是起始状态,而是采取的策略。即值函数是关于策略的函数。
- 可以这样理解这个式子:
状态值函数 = $\sum$ [在各种 $x$ 状态下选各种 $a$ 的概率 状态变化的概率 ( 状态变化带来的奖赏 + 之前的奖赏的部分折扣)],含义是包含多重情况的期望 - 这样的递归式子称为 Bellman等式
(可以暂时忽略数学推导的部分)
可以看出,想要计算 $V^{\pi}_T(x)$,我们可以从单步奖赏出发,通过迭代计算 $V_2^{\pi}$…并不断继续,对于 $T$ 步累计奖赏,只需要迭代 $T$ 轮就可以精确的计算出值函数。
同样的有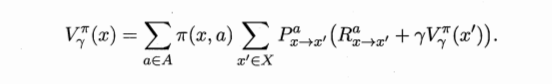
对于$V^{\pi}_{\gamma}(x)$,我们需要迭代次数设置一个停止准则,通常的情况是设置一个阈值 $\theta$,当每次迭代前后 $\triangle T \geq \theta $ 时进行计算,反之则停止
于是我们也可以得到状态-动作值函数
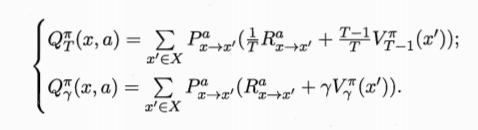
至此我们得到了量化 $V$ 和 $Q$ 的手段,下面我们基于策略评估着手改进我们的策略,即策略改进
策略改进
继续给出几个这部分讨论的对象
- 我们的目的是得到:$\pi^*=\arg\max\sum_{x\in X}V^{\pi}(x)$,即最大化累计奖赏
- 对应得到的值函数为:$\forall x\in X:V^(x)=V^{\pi^}(x)$,即最优策略对应的值函数
- 注意上式要求策略空间中没有约束的,如果我们采取了违背约束的动作以获得最大累计奖赏,这样获得的策略是有问题的
为了获得最优的策略,即获得最优的状态值函数,我们继承之前单步奖赏最大化模型的思路,有:
将所有动作求和改为 每一步选取奖赏最大化的动作,这样得到上式的最优化版本:
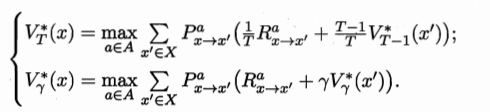
- 之前计算的是各种 $x$ 状态下选各种 $a$ 的概率 $\pi(x,a) (\sum = 1)$ 后乘对应情况的奖赏值之和,在我们取最优的条件下,所有非最优情况 $\pi(x,a)$ 置为0,把最优情况前的概率 $\pi^*(x,a)$ 置为1,(最优情况则是$\pi(x,a)$后面的奖赏部分计算值最大)。所以之前式子第一个求和式子消失了。
- 因为我们选取了最优动作,$V^(x)$ 就和最大的 $Q(x,a)$对应了(即当前的状态值函数直接和状态-动作函数挂钩),既有
$$ V^(x) = max_{a\in A}Q^{\pi ^*}(x,a)$$
(暂时理解不能可以忽略)
于是可以得到最优的 $Q$: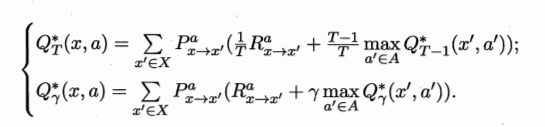
- 上述关于最优值函数的等式,称作最优Bellman等式
我们基于 每一步选取奖赏最大化的动作 进行策略的优化,从数学角度可以印证,我们的考虑是正确的,我们的策略:每一次选最优状态值对应动作,能够让总的值函数不断递增以达到最大,值函数关于策略的优化是单调递增的(略去证明)
此时我们有
$$\pi’(x) = \arg\max_{a\in A} Q^{\pi}(x,a)$$
通过对已有参数的计算,我们可以算出所有 $x$ 状态下所有的$Q(x,a)$的值,选取最大的$x$,作为我们的策略。
策略迭代和值迭代
- 先回顾一下之前两部分的内容:
- 对策略评估:
- 给出了值函数的迭代计算式,为量化提供了标准
- 根据迭代式可以看出,值函数是关于策略的函数
- 对策略优化:
- 我们采取每一步选取奖赏最大化的动作作为我们的策略的优化
- 且这种优化方式能稳定带来值函数的递增(数学部分略去)
- 让我们量化一下一些参数:
- $\pi(x,a)$ 可以看作 $|X|\times|A|$的矩阵,第$(x_i,a_j)$个位置的意义是在状态 $x_i$ 选取 $a_j$ 动作的概率
- $Q(x, a)$ 也是 $|X|\times|A|$的矩阵
- $\pi(x)$ 可以看作 $|X|\times1$的矩阵,第$(x_i,1)$个位置的意义是在在状态 $x_i$选取的动作(不是概率)
- $V(x)$ 也是 $|X|\times1$的矩阵
上面讨论了评估策略和优化策略的方法,下面我们可以给出求解最优策略的方法。
- 策略迭代:(通过优化策略的方法得到最大的值函数,此时的策略为最优策略)
- 根据上面的讨论,我们能很自然的得到策略迭代的优化方法,基本思路如下:
- 初始化:$\forall x\in X, V(x)=0, \pi(x,a)=\frac{1}{|A(x)|}$(开始的策略为随机选择)
- 评估策略:利用bellman等式计算 $V_T(x)$
- 优化策略:$\forall x\in X,\pi_{new}(x)=\arg\max_{a\in A} Q(x,a)$(选取奖赏最大化的动作)
- 判断是否停止循环,不停止回到2
- 得到最优策略 $\pi$
- 上面的算法核心在第三步优化策略,这也是“策略迭代”名字的由来,不过每次改进策略后都要重新进行策略评估,这通常很费时
之前我们提到,策略改进能稳定带来值函数的增加,值函数关于策略是单调递增的,所以我们直接最大化值函数$V(x)$ 来获得策略,这就是值迭代:
- 上面的算法核心在第三步优化策略,这也是“策略迭代”名字的由来,不过每次改进策略后都要重新进行策略评估,这通常很费时
- 值迭代:(直接优化值函数得到最大值函数,根据最大值函数得到最优策略)
- 初始化:$\forall x\in X, V(x)=0$
- 根据最优bellman等式优化 $V(x)$
- 判断是否停止循环,不停止回到2
- 得到最优策略:$\pi_{new}(x)=\arg\max_{a\in A} Q(x,a)$
以上就是关于有模型学习的讨论
Step 4: 免模型学习
蒙特卡罗强化学习
与有模型学习相比,免模型学习对环境一无所知,我们先讨论未知环境带来的问题:
- 策略无法评估:之前bellman等式的展开需要已知转移概率 $P$ 和奖赏 $R$ 进行全概率展开。在模型未知的情况下,我们进行模型评估的方法失效了。
- 策略迭代算法估计的是状态值函数 $V$,最终策略是通过状态-动作函数 $Q$ 获得。在模型未知的情况下,很难从 $V$ 直接转换到 $Q$。
- 由于环境未知,我们并不知道 $X$ 中有多少状态。(这直接影响了我们对策略$\pi$的初始化)
基于上面的问题,我们给出对应的解决方法:
- 和K摇臂赌博机一样,用平均累计奖赏近似代替期望累计奖赏(这称作蒙特卡罗强化学习)。当然,由于采样为有限次数,此方法更适用于T步累计奖赏的强化学习任务
- 直接估计 $Q$ 而非 $V$
- 在探索中逐渐发现状态并估计 $Q$
下面我们先介绍蒙特卡罗强化学习:
下面我们解释一下这个算法:
- 为了计算状态-动作函数,我们先进行采样,即第3行产生轨迹
- 评估策略时,(第6行)遵循了$\epsilon$贪心算法的思路,计算平均累计奖赏
- 优化策略时,(第9行)我们将原始策略结合$\epsilon$贪心得到:
$$\pi^{\epsilon}(x) =
\begin{cases}
\pi(x) \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad 以概率 1-\epsilon \
A中以均匀概率选择的动作\quad\space 以概率 \epsilon\
\end{cases}
$$
这样设计的策略可以让每个动作都有可能被选取,多次采样可以产生不同的采样轨迹
- 我们注意到,上述有两处引入的 $\epsilon$ 贪心:
- 评估策略时用平均累计奖赏近似值函数,这是$\epsilon$ 贪心的策略
- 优化策略时将原始策略与$\epsilon$ 贪心的策略结合
- 这样的算法,被评估的策略和被改进的策略是同一个函数,称为:同策略(on-policy)蒙卡罗特强化学习算法
当然,我们希望优化的算法就是原始策略而非$\epsilon$ 贪心的策略,同时也希望保有原来评估策略的方法,于是便有了异策略(off-policy)蒙卡罗特强化学习算法:
当优化的策略和评估的策略不相同时,看似并不能起到优化作用,实际上并非如此。可以从数学的角度上分析,通过对同策略算法中的奖赏$R$乘以一个系数,就能将原本$\epsilon$ 贪心策略中计算的值函数的期望变为原始策略的期望(略去证明,此处涉及到重要性采样知识)。即上述算法中的第6行所显示的。
同样的,因为优化策略为原始策略,第10行也做了相应变化。
时序差分学习
蒙特卡罗强化学习需要在一轮采样之后才进行值函数估计,我们之前在有模型学习下引入的策略迭代和值迭代算法可以基于bellman等式,在每一步采样之后就进行值函数估计,基于这样的想法,我们引入时序差分学习。
(此部分可以掠过数学推导部分,可以看懂即可)
还记得这个式子吗?(可以回顾之前的内容)
$$Q_n(k) = \frac{1}{n}((n-1)\times Q_{n-1}(k) + v_n)$$
我们也可以在这个基础上得到增量式计算值函数的公式:
- 对于状态-动作对$(x,a)$,不妨假定基于 $t$ 个采样已经估计出值函数
$Q_t^{\pi}(x,a)=\frac{1}{t}\sum_{i=1}^tr_i$ ,在得到第 $t+1$ 个采样 $r_{t+1}$ 时,代入上式有:
$$Q_{t+1}^{\pi}(x,a) = Q_{t}^{\pi}(x,a) +[\frac{1}{t+1}(r_{t+1}-Q_{t}^{\pi}(x,a))]$$
式中括号部分则为 $Q$ 值变化要加的增量。
此外更一般的,将 $\frac{1}{t+1}$ 可以替换为系数 $\alpha_{t+1}$,则增量为$\alpha_{t+1}(r_{t+1}-Q_{t}^{\pi}(x,a))$,在实践中通常令 $\alpha_{t}$ 为一个较小的正数 $\alpha$,将它看作一个累计奖赏的衰减系数,$\alpha$ 越大,越靠后的累计奖赏越重要。
上式是单步奖赏最大化问题中引入的迭代式,下面我们用bellman等式来计算多步奖赏最大化问题中的迭代式
以$\gamma$ 折扣累计奖赏为例,有
$$Q_{t+1}^{\pi}(x,a) = Q_{t}^{\pi}(x,a) +\alpha(R^{\alpha}_{x\to x’}+ \gamma Q^{\pi}_t(x’,a’) -Q_{t}^{\pi}(x,a))$$
其中 $x’$ 时前一次在状态 $x$ 执行 $\alpha$ 后转移到的状态,$a’$ 是策略 $\pi$ 在 $x’$ 上选择的动作。
现在我们有了增量计算值函数的手段,下面引入 Sarsa 和 Q-learning

此算法名字的由来,是因为每次更新值函数需要知道前一步的状态(state),前一步的动作(action),奖赏值(state),当前状态(state),将要执行的动作(action),由此得名 Sarsa算法
此算法为同策略算法:第5行,第6行都是 $\epsilon$ 贪心策略
与之对应的Q-learning则是异策略算法:
第6行都是 $\epsilon$ 贪心策略,第5行是原始策略。
强化学习入门到此结束~